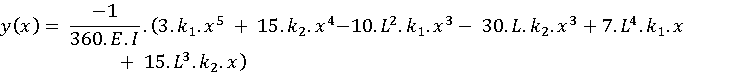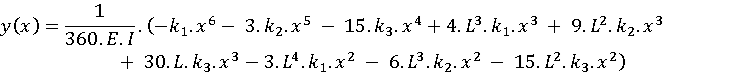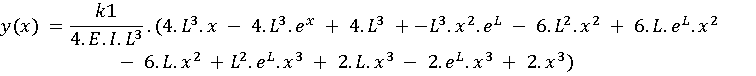TIC COM APLICAÇÃO DO MÉTODO DAS DIFERENÇAS FINITAS PARA ANÁLISE DA LINHA ELÁSTICA EM VIGAS COM CONDIÇÕES DE CONTORNO DIVERSAS E SUJEITA A CARGA VARIÁVEL

ICT WITH APPLICATION OF THE FINITE DIFFERENCE METHOD FOR ELASTIC LINE ANALYSIS IN BEAMS WITH DIFFERENT BOUNDARY CONDITIONS AND SUBJECT TO VARIABLE LOAD

(1 espaço)

FRANCISCO, Caio H. Acilino^1,2; BOMBO, Lucas Gabriel^2,3; SABINO, Marcio Rodrigues^,4,5; 

¹ Engenheiro Mecânico pelo Centro Universitário da Fundação Hermínio Ometto - FHO;

² Tecnólogo em Projetos Mecânicos pela Faculdade de Tecnologia de São Paulo – FATEC;

³ Engenheiro Mecânico pelo Instituto Federal – IFSP unidade Piracicaba;

⁴ Professor Mestre do Curso de Engenharia Mecânica – Fundação Hermínio Ometto - FHO;

⁵ Professor Mestre do Curso de Projetos Mecânicos Faculdade de Tecnologia de São Paulo – FATEC – Unidade Mogi Mirim;

caiohenrique819@alunos.fho.edu.br

 (1 espaço)

RESUMO. A previsão da deformação de vigas é fundamental para o dimensionamento seguro de estruturas. Diversos fatores influenciam essa deformação, como geometria, material, condições de contorno e carregamentos. O objetivo principal deste trabalho foi modelar as equações da linha elástica para quatro casos de vigas com diferentes tipos de carregamento pelo método numérico das diferenças finitas (MDF) e analisar os resultando comparando-os com as soluções analíticas. Como objetivo secundário, desenvolver uma ferramenta digital de Tecnologia da Informação e Comunicação (TIC) para a análise das vigas. As equações diferenciais da linha elástica foram modeladas, resolvidas analiticamente e numericamente pelo MDF. Foi desenvolvida uma TIC educacional na linguagem de programação Python e a comparação entre os resultados numéricos e analíticos foram realizados por meio de análise dos erros máximos absolutos. A análise de erros demonstrou concordância entre os resultados analíticos e numéricos, validando a sua aplicabilidade em diferentes cenários. A TIC demonstrou ser uma excelente ferramenta educacional digital capaz tornar o processo mais dinâmico, interativo, personalizado, robusto e confiável nos resultados.

(1 espaço)

Palavras-chave: equação da linha elástica; diferenças finitas; métodos numéricos. TIC.

 (1 espaço)

ABSTRACT. Predicting beam deformation is essential for the safe design of structures. Several factors influence this deformation, such as geometry, material, boundary conditions and loads. The main objective of this work was to model the elastic line equations for four cases of beams with different types of loading using the numerical method of finite differences (FDM) and analyze the results by comparing them with the analytical solutions. As a secondary objective, develop a digital Information and Communication Technology (ICT) tool for beam analysis. The differential equations of the elastic line were modeled, solved analytically and numerically by FDM. An educational ICT was developed in the Python programming language and the comparison between numerical and analytical results was carried out through analysis of the maximum absolute errors. Error analysis demonstrated agreement between analytical and numerical results, validating its applicability in different scenarios. ICT declared itself to be an excellent digital educational tool capable of making the process more dynamic, interactive, personalized, robust and reliable in results.

(1 espaço)

Keywords: Elastic line equation; finite differences; numerical methods; ICT.

INTRODUÇÃO

            A análise estrutural é uma área importante das engenharias em geral. Um dos principais elementos utilizados na construção de estruturas é a viga, o que faz o conhecimento em relação as suas tensões e deformações, um dos principais objetivos da resistência dos materiais.

Além das tensões, uma grandeza importante de uma viga é sua deflexão, que consiste em uma deformação que ela apresenta em seu eixo longitudinal, quando submetida a uma carga transversal (HIBBELER, 2011).

A equação da linha elástica de uma viga caracteriza a forma da viga deformada após a aplicação de uma força ou carregamento. Segundo Beer (2011), quando uma viga prismática suporta uma força distribuída  em seu comprimento, têm-se que sua linha elástica é governada por uma equação diferencial linear de quarta ordem dada pela equação (1.0):

(1.0)

onde,  é o módulo de elasticidade do material em que a viga é feita (para vigas de material homogêneo o módulo de elasticidade é constante) e  trata-se do momento de inércia da viga, a qual, para vigas prismáticas e sem alteração de altura, também possui o seu valor constante.

Conhecendo-se a força cortante sobre uma posição  da viga, é possível determinar a equação da linha elástica como descrito pela EDO (1.1):

(1.1)

Por meio da EDO (1.2), conhecendo-se a função do momento fletor em qualquer ponto  da viga, a linha elástica pode ser obtida por

(1.2)

Por fim, a EDO (1.3) relaciona o ângulo tangente à equação da linha elástica :

(1.3)

O método das diferenças finitas é utilizado para resolução de equações diferenciais e consiste em transformar uma derivada em uma aproximação de diferenças finitas, que são obtidas aplicando uma expansão da Série de Taylor (ALVES, 2007; RUGGIERO, 1988; SOARES, 2010; SABINO, 2023). Neste método, o domínio de uma equação diferencial é substituindo por diversos pontos discretos chamados de nós que apresentam um espaçamento  entre eles, que pode ser denominado com espaçamento da malha (RUGGIERO,1988; FAIRES, 2008; CHAPRA, 2008; SABINO, 2023).

Dada uma equação diferencial com um domínio no intervalo  e dividindo esse intervalo em  partes iguais, define-se o espaçamento  como em (1.4):

(1.4)

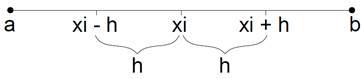
Considerando um ponto qualquer  no intervalo , um ponto antes será  e um ponto depois será  conforme representado na Figura 1.

Figura 1 - Representação do ponto  no domínio da equação diferencial.

Fonte: Próprio autor.

Dada uma função  e um ponto , deseja-se que a equação diferencial se aproxime desse ponto regressivamente. Assim, considerado uma expansão da série de Taylor em torno do ponto , com um erro truncado de ordem 2, aplicando o ponto  na função e isolando-se a primeira derivada, obtém-se a equação (1.5):

(1.5)

chamada de diferença finita atrasada.

Como para diferenças atrasadas, considerando uma função , e um ponto , deseja-se que a equação diferencial se aproxime desse ponto progressivamente. Novamente, considerado uma expansão da série de Taylor em torno do ponto  com um erro truncado de ordem 2 e agora aplicando o ponto  na função e isolando-se a primeira derivada, obtém-se a equação (1.6):

(1.6)

chamada de diferença finita avançada.

Como nas diferenças atrasada e avançada, considerando uma função , e um ponto , deseja-se que a equação diferencial se aproxime desse ponto por meio dos pontos  e . Novamente, considerado uma expansão da série de Taylor em torno do ponto  com um erro truncado de ordem 2 Aplicando os pontos na função e isolando-se a primeira derivada, obtém-se a equação (1.7):

(1.7)

chamada de diferença finita centrada, que geometricamente é representa pela Figura 2:

Figura 2 - Representação geométrica para diferenças finitas centradas.

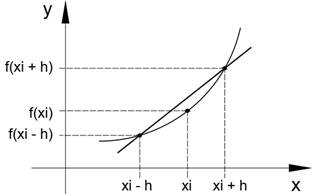
Fonte: Próprio autor.

Essa aproximação é mais precisa em relação as outras duas apresentadas, pois apresenta um truncamento de ordem 3 (ALVES, 2007; RUGGIERO,1988; SOARES, 2010).

As expansões da série de Taylor aplicadas nos pontos  e , com erros na ordem 4, seguem conforme as equações (1.8) e (1.9) (ALVES, 2007; SOARES, 2010):

	(1.8)
	(1.9)

Segundo Alves (2007) e Soares (2010), para aproximar uma derivada de segunda ordem em diferenças finitas, soma-se as equações (1.8) e (1.9) e isola-se a segunda derivada obtendo-se a equação (1.10):

(1.10)

Para aproximar uma deriva de terceira ordem com diferenças finitas, aplica-se a equação (1.7) na equação (1.10), obtendo a equação (1.11) (ALVES, 2007; SOARES,2010):

(1.11)

A aproximação de uma derivada de quarta ordem em diferenças finitas pode ser obtida aplicando-se a equação (1.10) nela mesma, gerando a equação (1.12) (ALVES, 2007; SOARES, 2010):

(1.12)

Como visto, a deflexão pode ser determinada por meio de métodos analíticos fornecendo uma solução exata do problema. Entretanto, existem casos em que as vigas formam uma estrutura muito complexa, sendo a resolução numérica uma boa estratégia para a resolução do problema (SILVA, 2011).

As Tecnologias da Informação e Comunicação (TICs) são ferramentas digitais que remodelam o ensino-aprendizagem. Por meio de softwares, plataformas online e recursos multimídia, as TICs buscam tornar as aulas mais envolventes, participativas e individualizadas, promovendo o engajamento dos alunos e ampliando o acesso à educação de qualidade.

(1 espaço)

Poucas  inovações  tecnológicas  provocaram  tantas  mudanças  em tão pouco tempo na sociedade como as novas tecnologias de informação e comunicação –TIC.  Dentro  dessas  mudanças  está  incluída  a  educação. Novas  maneiras  de  pensar  e  conviver  estão  sendo  elaboradas  no  mundo das telecomunicações e da informática (LÉVY, 1998, p.24).

(1 espaço)

O objetivo principal deste trabalho foi  modelar as equações da linha elástica para quatro condições de contorno para casos de vigas com diferentes tipos de carregamento utilizando o método numérico das diferenças finitas (MDF). Por meio dessa modelagem, buscou-se analisar os resultados obtidos e compará-los com as soluções analíticas para validar a viabilidade do método numérico para este tipo de problema. Como objetivo secundário, foi proposto o desenvolvimento de uma TIC implementada na linguagem de programação Python para a análise das vigas estudadas.

MÉTODOLOGIA

            Nesta seção, são desenvolvidas e apresentadas as equações da linha elástica para quatro casos de vigas escolhidas para o estudo, sendo: uma viga engastada livre submetida a uma um carregamento constante, uma viga bi-apoiada submetida a um carregamento linear, uma viga bi-engastada submetida a um carregamento quadrático e uma viga engastada e apoiada submetida a um carregamento exponencial. Para cada viga foi determinada a equação da linha elástica, utilizando métodos analíticos resolvendo as EDO presentes de (1.0) a (1.3) e métodos numéricos utilizando as aproximações por diferenças finitas. A solução analítica dará a base comparativa para validação da solução numérica.

Para obter-se a modelagem numérica, inicialmente, como indicado na equação (1.13), divide-se o comprimento  das vigas analisadas em  nós com espaçamentos iguais: 

(1.13)

a qual definirá o comprimento de cada subintervalo da malha do domínio numérico.

Substituindo a equação (1.12) na equação (1.0), obtém-se a equação

(1.14)

da qual isolando o  para o lado direto da equação e chamando esta parcela de  obtém-se:

(1.15)

Uma outra simplificação será expressa na equação (1.16)

(1.16)

a qual facilitará as notações matriciais a serem desenvolvidas.

VIGA ENGASTADA LIVRE SUBMETIDO A UM CARREGAMENTO CONSTANTE

Considere uma viga engastada-livre, submetida a um carregamento  constante e com condições de contorno dadas em (1.17) e (1.18)

	(1.17)
	(1.18)

Ela sofrerá uma deflexão e o seu perfil como ilustrado na Figura 3.

Figura 3 - Viga engastada sobre um carregamento constante.

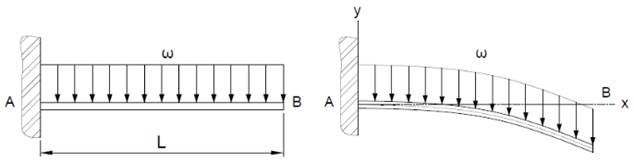
Fonte: Próprio autor.

Após analisar o diagrama de corpo livre (D.C.L) do esquema presente na Figura 3 com todas as forças atuantes e calculando-se as reações de apoio, momento e momento fletor sob as condições de contorno apresentadas e resolvendo a equação diferencial da linha elástica dada pela equação (1.0), obtém-se a equação (1.19):

(1.19)

Para a viga engastada livre, seu domínio pelo método das diferenças finitas, será discretizado em  pontos igualmente espaçados com comprimento . O ponto da extremidade engastada é  e o ponto da extremidade livre da viga é , conforme representado na Figura 4.

Figura 4 - Representação da viga engastada discretizada em  nós.

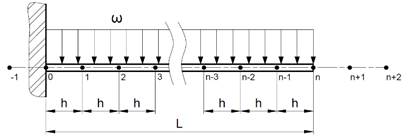
Fonte: Próprio autor.

Os pontos ,  e , são pontos imaginários utilizados para definir as equações nos extremos da viga. Primeiramente são determinadas as condições de contorno da viga engastada com o intuito de diminuir o número de variáveis na modelagem da equação da linha elástica. Assim considerando a condição de contorno (1.18) e  um ponto inicial da viga localizado no ponto  têm-se (1.20):

(1.20)

Agora considerando a equação (1.3) e aplicando uma aproximação por diferenças finitas centradas conforme (1.7) têm-se a equação (1.21):

(1.21)

e aplicando a condição de contorno (1.17) obtém-se (1.22):

(1.22)

O lado livre da viga engastada não apresenta momento fletor  e nem uma força cortante . Com isso para esse lado têm-se as condições de contorno (1.23) e (1.24):

	(1.23)
	(1.24)

Aplicando uma aproximação por diferenças finitas de segunda ordem na  condição (1.23), conforme  (1.10) e isolando têm-se (1.25):

(1.25)

E aplicando uma aproximação por diferenças finitas de terceira ordem, conforme a (1.11), na condição (1.24) têm-se a equação (1.26):

(1.26)

Definido as equações das condições de contorno, é determinado a equação da linha elástica por diferenças finitas para cada ponto da viga. Considerando os pontos de contorno da viga têm-se para , que é o ponto engastado sem deflexão, substituído nas equações (1.20) e (1.22) tem-se as equações (1.27) e (1.28):

	(1.27)
	(1.28)

Para , que é o ponto livre da viga, substituído nas equações (1.25) e (1.26) obtêm-se as equações (1.29) e (1.30):

	(1.29)
	(1.30)

Substituindo (1.29) na (1.30) têm-se a equação (1.34):

(1.31)

Definido as equações para cada ponto da viga se obtém um sistema linear do tipo  de acordo com (1.32):

(1.32)

VIGA BI-APOIADA SUBMETIDA A UM CARREGAMENTO LINEAR

Considere uma viga bi-apoiada submetida a um carregamento linear do tipo                         , representada pela Figura 5.

Figura 5 - Viga bi-apoiada sobre um carregamento linear.

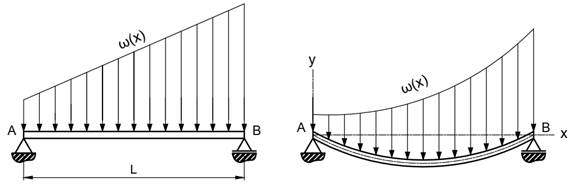
Fonte: Próprio autor.

Utilizando as condições de contorno (1.33), (1.34) e a aplicando as devidas integrais na equação (1.0) obtém-se a equação da deflexão da viga (1.35):

		(1.33)
		(1.34)
			(1.35)

A equação (1.35) representa a equação da linha elástica para qualquer valor de x, de uma viga bi-apoiada submetida a um carregamento linear.

Como foi feito na viga engastada livre, será determinado para viga bi-apoida, o seu domínio pelo método das diferenças finitas discretizado em  pontos igualmente espaçados de . Um dos pontos apoiados é  e o outro é , conforme representado na Figura 6.

Figura 6 - Representação da viga bi-apoida discretizada em  nós.

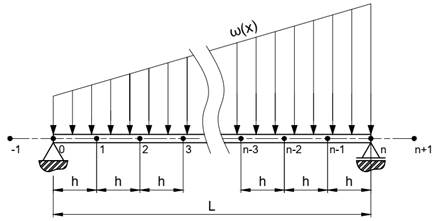
Fonte: Próprio autor.

onde os pontos  e , são pontos imaginários utilizados para definir as equações nos extremos da viga.

Definido as equações para cada ponto da viga se obtém o sistema linear  (1.36):

(1.36)

VIGA BI-ENGASTADA SUBMETIDA A UM CARREGAMENTO QUADRÁTICO

Para o próximo problema será considerado uma viga bi-engastada submetida a um carregamento quadrático , representada abaixo pela Figura 7, cujas condições de contorno são apresentadas em (1.37), (1.38), (1.39) e (1.40):

Figura 7 - Viga bi-apoiada sobre um carregamento constante.

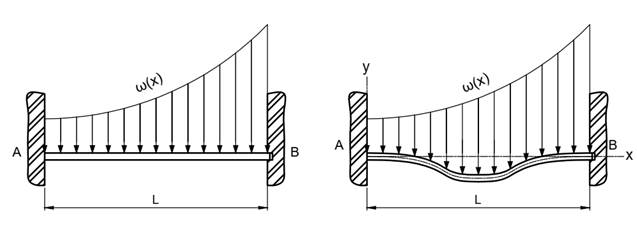
Fonte: Próprio autor.

	(1.37)
	(1.38)
	(1.39)
	(1.40)

A equação (1.41) representa a equação da linha elástica para qualquer valor de x, para uma viga bi-engastada submetida a um carregamento quadrático.

(1.41)

Como nas vigas anteriores, será determinado as equações da deflexão da viga aplicando o método das diferenças finitas discretizada em  pontos, onde os pontos  e  são engastados conforme a Figura 8.

Figura 8 - Representação da viga bi-engastada discretizada em  nós.

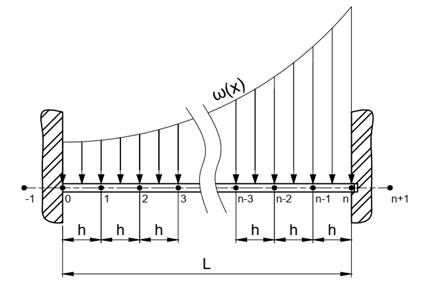
Fonte: Próprio autor.

Definido as equações para cada ponto da viga se obtém um sistema linear do tipo       conforme (1.42):

(1.42)

VIGA ENGASTADA E APOIADA COM CARREGAMENTO EXPONENCIAL

Por último vamos considerar o problema com uma viga engastada em uma extremidade e apoiada na outra extremidade, submetida a um carregamento exponencial , conforme a Figura 9.

Figura 9 - Viga engastada e apoiada sobre um carregamento constante.

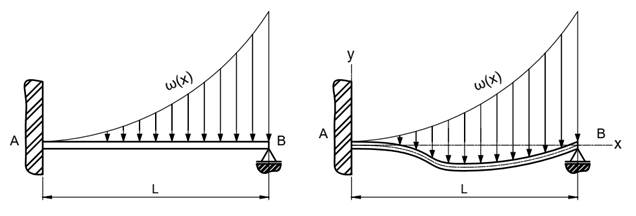
Fonte: Próprio autor.

DIAGRAMA DE CORPO LIVRE (D.C.L)

A Figura 10 apresenta o diagrama de corpo livre da viga engastada e apoiada e todas as forças que atuam na viga. As condições de contorno são dadas em (1.43), (1.44) e (1.45):

	(1.43)
	(1.44)
	(1.45)

Aplicando as devidas integrais na equação (1.0), obtém-se a equação da linha elástica para qualquer valor de , para uma viga engastada e apoiada (1.46):

(1.46)

Por fim, será determinado as equações da deflexão para uma viga engastada e apoiada, pelo método das diferenças finitas discretizada em  pontos, onde os pontos  é o ponto engastado e  é o ponto apoiado, conforme a Figura 10.

Figura 10 - Representação da viga engastada e apoiada discretizada em  nós.

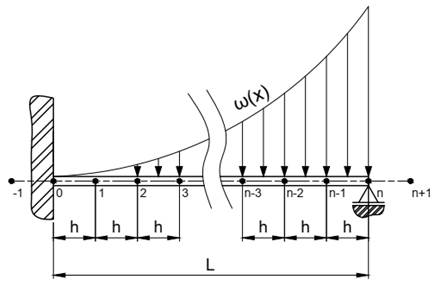
Fonte: Próprio autor.

Definido as equações para cada ponto da viga se obtém um sistema linear do tipo  conforme (1.47):

(1.47)

IMPLEMENTAÇÃO NUMÉRICA

A implementação numérica foi realizada na linguagem de programação Python pelo seu poder sintético estruturado para a escrita de scripts (OLIVEIRA NETO, CAGNIN, CANCIGLIERI, 2020; OLIVEIRA NETO, CAGNIN, CANCIGLIERI, 2021). Aproveitando as principais funcionalidades da linguagem, foi possível utilizar os pacotes numpy e sympy, respectivamente para ferramentas numéricas e simbólicas dentro da linguagem Python, possibilitando a confecção de uma forte ferramenta para resolução de problemas de deflexão de vigas dentro das engenharias.

Com base nas equações diferenciais (1.0), (1.1), (1.2) e (1.3), foi possível implementar as suas resoluções analíticas simbólicas. Buscou-se a confecção de um algoritmo adaptável ao tipo de condições de contornos de uma viga engastada livre, bi-apoiada, bi-engastada e engastada-apoiada, podendo escolher entre carregamentos do tipo constante, linear, quadrático e exponencial. Os valores do comprimento  da viga, Módulo de elasticidade  e momento de inércia  também podem ser inseridos pelo usuário.

A implementação via método das diferenças finitas aborda todas as combinações entre as condições de contorno e tipos de carregamentos implementados para o método analítico descrito anteriormente. Nela, o usuário também pode inserir o número de nós com o qual deseja realizar as simulações. Assim, o algoritmo irá construir o sistema linear penta diagonal correspondente, resolvê-lo aproveitando a sua estrutura e apresentará o vetor solução de maneira numérica e gráfica.

Com o intuito de facilitar a um usuário a obtenção dos resultados e a possibilidade de outras combinações de carregamentos e condições de contorno, utilizou-se conceitos de TIC com um foco educacional, desenvolvendo-se  um software aproveitando-se pacotes visuais da linguagem Python, evoluindo a implementação para uma ferramenta com interfaces gráficas do usuário (GUI – Graphic User Interface).

De maneira ilustrativa, serão apresentadas na sequência, simulações realizadas na TIC desenvolvida para alguns dos casos propostos, realizando um comparativo qualitativo gráfico com os resultados analíticos e um quantitativo em relação a norma infinita em relação a cada nó discretizado.

RESULTADOS E DISCUSSÃO

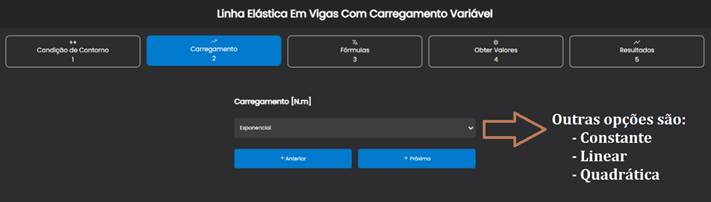
A TIC desenvolvida possui um visual simples e intuitivo com menus superiores para o usuário realizar a escolha da Condição de Contorno, do Carregamento, dos parâmetros da Fórmula do carregamento, dos parâmetros e características geométricas e de material da viga no submenu Obter Valores e por fim um submenu de Resultados. A Figura 11 ilustra a inserção de um carregamento do tipo exponencial, tendo outras opções de escolha como de um carregamento constante, linear e quadrático.

Figura 11 – Inserindo o tipo de carregamento.

Fonte: Próprio autor.

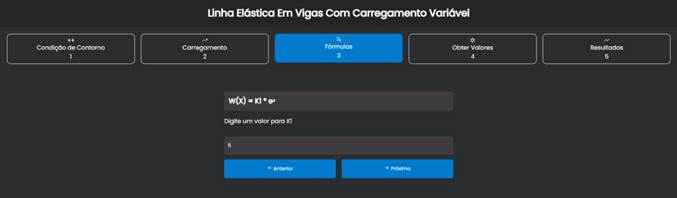
A Figura 12 ilustra o usuário inserindo os valores dos parâmetros da fórmula do carregamento idealizado sobre a viga.

Figura 12 – Inserção dos parâmetros.

Fonte: Próprio autor.

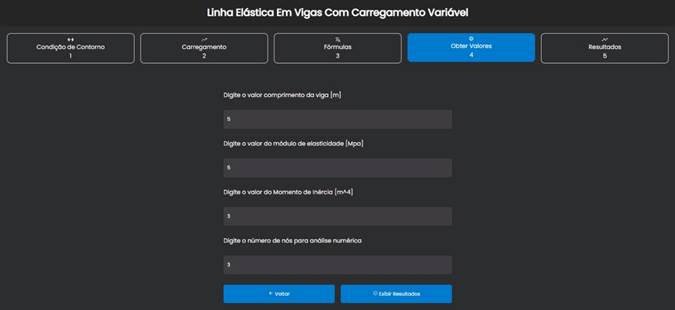
A Figura 13 ilustra a inserção dos valores que darão as características da viga como comprimento, módulo de elasticidade, momento de inércia, além do número de nós desejados na simulação por MDF.

Figura 13 – Características da Viga e condição de simulação para o MDF.

Fonte: Próprio autor.

A inserção da condição de contorno está ilustrada na Figura 14, na qual o usuário tem a sua disposição as vigas bi-apoiada, bi-engastada, engastada-livre e engastada-apoiada.

Figura 14 – Inserção da condição de contorno.

Fonte: Próprio autor.

Ao clicar no submenu Resultados, o usuário terá um descritivo das variáveis de entrada utilizadas, o resultado do erro absoluto máximo comparativo entre a solução analítica e a numérica pelo MDF e os gráficos do comportamento das deflexões também pelos dois métodos.

Figura 15 – Resultados da simulação.

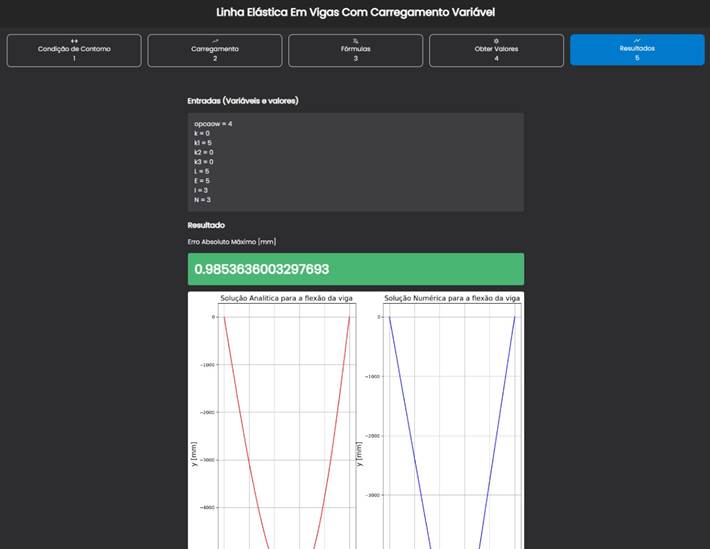
Fonte: Próprio autor.

Para uma visualização dos resultados obtidos, serão apresentados algumas das simulações possíveis de serem realizadas. Para as simulações numéricas, foram analisadas as deflexões para quatro casos de vigas: Uma viga engastada livre submetida a uma um carregamento constante ; uma viga bi-apoiada com um carregamento linear ; uma viga bi-engastada submetida a um carregamento quadrático  e uma viga engastada e apoiada submetida a um carregamento exponencial  . O material das vigas estudadas será o Perfil W460 x 158 de aço estrutural (ASTM-A36) e tal material apresenta as características apresentadas na Tabela 1.

Tabela 1 - Valores das propriedades do material da viga.

Propriedade	Sigla	Unidade	Valor
Módulo de elasticidade	E
Momento de inércia	I

Fonte: (BEER, 2011).

VIGA ENGASTADA LIVRE SUBMETIDA A UM CARREGAMENTO CONSTANTE

Para uma análise qualitativa para os resultados das deflexões no caso da viga engastada livre submetida a um carregamento constante, a Figura 16 representa a solução analítica da deflexão de uma viga de comprimento   e a solução numérica para 500 nós.

Figura 16 - Solução analítica e numérica da viga engastada para 500 nós.

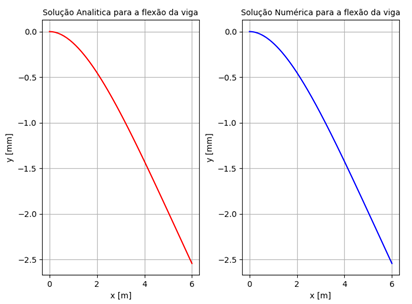
Fonte: Próprio autor.

Na Figura 16, devido a escala, fica imperceptível a diferença qualitativa das curvas analíticas e numéricas. Assim, para a análise quantitativa, a Quadro 1 apresenta valores do máximo erro absoluto entre a solução numérica e a analítica, por meio da norma infinita, para diferentes quantidades de nós na discretização.

Quadro 1 - Máximo erro absoluto entre solução analítica e numérica.

Números de nós	[mm]
10	5,358686 x 10^-2
50	4,565767 x 10^-3
100	1,604116 x 10^-3
250	4,043494 x 10^-4
500	1,485749 x 10^-4

Fonte: Próprio autor.

Verifica-se que para 500 nós, quantidade utilizada na simulação da Figura 16, que o erro absoluto máximo obtido dentro do domínio  da viga foi de aproximadamente . Esta precisão pode ser melhorada aumentando-se o número de nós na discretização do modelo.

VIGA BI-APOIADA COM UM CARREGAMENTO LINEAR

Aplicando uma discretização com 500 nós na viga bi-apoiada, como foi feito na viga engastada, se obtêm um gráfico a direita da solução analítica na Figura 17.

Figura 17 - Solução analítica e numérica da viga bi-apoiada para 500 nós.

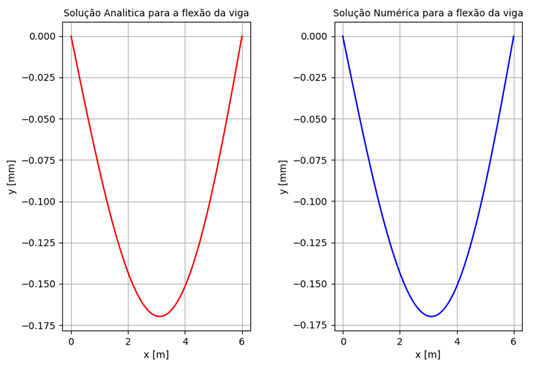
Fonte: Próprio autor.

Qualitativamente, as curvas obtidas para os resultados analíticos e numéricos são muito próximas dentro da escala utilizada nos gráficos. O Quadro 2 mostra os máximos erros absolutos para cada nó analisado, possibilitando uma visão melhor da convergência que está ocorrendo entre os gráficos.

Quadro 2 - Máximo erro absoluto entre solução analítica e numérica.

Números de nós	[mm]
10	3,154938 x 10^-6
50	2,822042 x 10^-7
100	9,977418 x 10^-8
250	2,524127 x 10^-8
500	8,901815 x 10^-9

Fonte: Próprio autor.

Por meio do quadro 2 é possível observar que a solução numérica para viga bi-apoiada para 500 nós que o erro absoluto máximo obtido foi de aproximadamente , valor extremamente baixo relativamente ao domínio  da viga simulada.

VIGA BI-ENGASTADA SUBMETIDA A UM CARREGAMENTO QUADRÁTICO

Assim como nas vigas anteriores, foi aplicado uma descritização com 500 nós na viga bi-engastada e o comportamento está ilustrado qualitativamente nos gráficos da Figura 18.

Figura 18 - Solução analítica e numérica da viga bi-engastada para 500 nós.

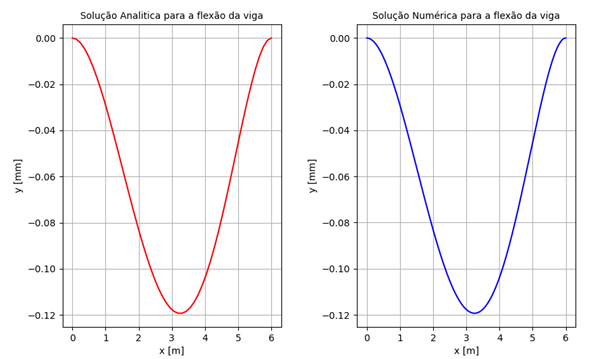
Fonte: Próprio autor.

A convergência do gráfico da solução numérica para analítica é melhor representada com os máximos erros absolutos para cada nó apresentado no Quadro 3.

Quadro 3 - Máximo erro absoluto entre solução analítica e numérica.

Números de nós	[mm]
10	2,322486 x 10^-5
50	2,092946 x 10^-6
100	7,401383 x 10^-7
250	1,872540 x 10^-7
500	6,620658 x 10^-8

Fonte: Próprio autor.

Como no modelo bi-apoiado é possível observar no Quadro 3 a diminuição no erro com o aumento de número de nós da discretização, obtendo-se para 500 nós um erro absoluto máximo de .

VIGA ENGASTADA E APOIADA COM CARREGAMENTO EXPONENCIAL

Por fim, foi realizado uma discretização com diferentes quantidades de nós impostas no domínio   de uma viga engastada e apoiada submetida a um carregamento exponencial. Comparando o resultado numérico com o analítico, o quadro 4 apresenta os máximos erros absolutos ilustrando o que ocorre quando utilizados 10, 50, 100, 250 e 500 nós:

Quadro 4 - Máximo erro absoluto entre solução analítica e numérica.

Números de nós	[mm]
10	1,503415 x 10^-5
50	1,348365 x 10^-6
100	4,767923 x 10^-7
250	1,206244 x 10^-7
500	4,263443 x 10^-8

Fonte: Próprio autor.

Os gráficos apresentados na figura 19 possibilitam uma visualização qualitativa dos resultados quando utilizados 500 nós, com os quais foi obtido um erro absoluto máximo de  como ilustrado no quadro 4.

Figura 19 - Solução analítica e numérica da viga engastada e apoiada para 500 nós.

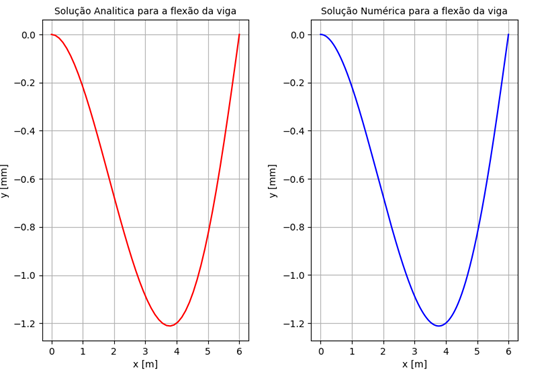
Fonte: Próprio autor.

CONCLUSÃO

Visto a importância do conhecimento da deformação que uma viga apresenta em seu eixo longitudinal quando submetida a carregamento transversal, o objetivo deste trabalho foi realizar a modelagem para o método das diferenças finitas, o desenvolvimento de uma ferramenta computacional na linguagem de programação Python e a análise da deflexão de quatro casos de vigas sujeitas a quatro possíveis condições de contornos e quatro tipos de carregamentos distintos compondo 16 cenários possíveis.

A TIC se destaca por sua interface amigável e intuitiva, permitindo que usuários com diferentes níveis de conhecimento técnico possam facilmente simular e analisar vigas. A precisão da TIC foi comprovada por meio da comparação entre as soluções analíticas e numéricas pelo método das diferenças finitas para vigas bi-apoiadas, bi-engastadas, engastada-apoiada e engastada-livre como condições de contorno sob os possíveis carregamentos constante, linear, quadrático e exponencial. Em todos os casos, a TIC apresentou erros absolutos máximos inferiores a 10^-4  quando utilizados 500 nós na simulação do MDF, sugerindo sua confiabilidade e robustez para a análise de vigas.

Um ponto crucial reside capacidade da ferramenta desenvolvida resolver problemas hiperestáticos, algo que soluções de outras famosas TICs de maneira online não o faz. Essa característica torna a TIC uma ferramenta ainda mais poderosa e versátil, ampliando significativamente o escopo de problemas que podem ser analisados.

Em resumo, o projeto apresenta-se como uma solução completa e confiável para a análise de deflexão de vigas, oferecendo vantagens como uma interface amigável e intuitiva, precisão nos resultados das deflexões para diferentes casos de vigas e cenários com carregamentos e condições de contorno, capacidade de resolver problemas hiperestáticos e facilidade de uso.

REFERÊNCIAS

ALVES, Lucas Máximo. Introdução aos métodos aproximados em Engenharia: Álgebra Linear, Geometria Analítica, Cálculo e Equações Diferenciais, Curitiba. 2007. 287 f. - Universidade Federal do Paraná Setor de tecnologia/setor de ciências exatas Departamento de engenharia civil/ Departamento de matemática, Curitiba, 2007.

APRENDER ENGENHARIA. Vigas Online. 2018. Disponível em: https://www.aprenderengenharia.com.br/viga-online. Acesso em: 10 ago. 2022.

BEER, F. P.; JR, E. R. J.; DEWOLF, J. T.; MAZUREK, D. F. Mecânica dos Materiais. 5. ed. – Porto Alegre: AMGH, 2011.

CHAPRA, S. C. Métodos numéricos para engenharia. 5 Ed. McGrw-Hill, 2008.

FAIRES, J. Douglas; BURDEN, Richard L.; Análise Numérica. 11. ed. Säo Paulo: Editora Cengage, 2008.

HIBBELER, R. C.. Estática: mecânica para engenharia. 12. ed. São Paulo: Pearson Prentice Hall, 2011.

LÉVY, P. As tecnologias da inteligência: o futuro do pensamento da era da informática. 34. ed. 1998.

OLIVEIRA NETO, Marcílio Francisco de; CAGNIN, Renato Luciano; CANCIGLIERI, Larissa de Oliveira Figueira. Programação de computadores I: uma abordagem com Python. 1. ed. Araras, SP: Fundação Hermínio Ometto-FHO/CEMAD, 2020. 125 p., il, 3.219 KB. ISBN 978-65-87752-12-9.

OLIVEIRA NETO, Marcílio Francisco de; CAGNIN, Renato Luciano; CANCIGLIERI, Larissa de Oliveira Figueira. Programação de computadores II: uma abordagem com Phyton. 1. ed. Araras, SP: Fundação Hermínio Ometto-FHO/CEMAD, 2021. 79p. (1.597 Kb), il. ISBN 978-65-87752-47-1.

RUGGIERO, M.A.G.; LOPES, V.L.R. Cálculo Numérico: Aspectos Teóricos e Computacionais. 2a Ed. São Paulo: Makron Books, 1988.

SABINO, Marcio Rodrigues. Métodos Numéricos para Engenharia. 1. ed. Araras, SP: Fundação Hermínio Ometto-FHO/CEMAD, 2023. 414p. (10.690 Kb), il. e-book. ISBN 978-65-6014-039-4.

SILVA, Selênio Feio da; SOARES, Alexandre Andrade Brandão. O MÉTODO DAS DIFERENÇAS FINITAS APLICADO À TEORIA DAS VIGAS. Revista Traços, Belém, v. 13, n. 27, p.9-23, jun. 2011.

SOARES, Alexandre Andrade Brandão – O método das diferenças finitas aplicado à teoria das vigas, Belém. 2010. 142 f. – Universidade da Amazônia, Belém, 2010.